Things That Roll

I’ll start this section with a fairly easy maze, one in which a single die rolls across a page. This will be a good introduction to the more complex mazes that follow, mazes where all kinds of weirdly-shaped objects roll across a page.

In all these mazes, you must first print out a full-size diagram. So click here to go to the diagram then print it. The picture at the right is just a small illustration of the maze.
After you’ve printed the diagram, place the die on the square marked Start, and position it so the face with the 6 is on top. Then tip the die from square to square (landing on white squares only) until you can land on the square marked Goal. (You might think of the die as a large carton that is too heavy to turn or slide, but you can tip it over on an edge and have it land in an adjacent square.)
There’s one restriction: you cannot tip onto a square if it results in the 1 being on top of the die. So, for example, from Start you could not move east, then north, then east. Click here for the solution. Small Version of Maze

I created this maze recently for the World Puzzle Championship. It was one of eighteen puzzles in an on-line qualifying exam used to pick the American team. That team will compete in the Championship to be held in Budapest in October, 1999. Will Shortz and Nick Baxter, who put together the exam, asked me to create a maze with a new layout, but with the same rules as one in my book SuperMazes.

Mazes with a single rolling die are now generally referred to as rolling-cube mazes, and they are pretty much an invention of mine. SuperMazes had four of them and even had a section called How to Create Your Own Rolling-Cube Mazes. That section turned out to be very popular. In John McCallion’s review of the book, he included a simple rolling-cube maze of his own creation. John’s maze wasn’t supposed to be especially challenging; he just wanted to show that it is possible to create these mazes.

Others have taken this concept of rolling cubes way beyond anything I had envisioned. Ed Pegg, Jr. created a maze that uses a cube with arrows on its faces. This cube rolls over a grid of arrows. To see his maze, go to Ed’s web site, www.mathpuzzle.com (which, incidentally, is the best puzzle site on the Internet), scroll down to “My Math Puzzle Pages,” then click on “Multistate Mazes.”

The greatest advance in this peculiar form of puzzle was made by Richard Tucker. He is a British software developer and puzzle designer. One of his creations is the 3D puzzle “King’s Court,” published by Pentangle.

Instead of a cube, Tucker uses two dice taped together! The dice form an elongated block that traces weird paths across the page. Instead of rolling, it looks more like it’s flopping around. It sounds like it should never work, but it does. The maze is easy to understand, though finding the solution can be hard.

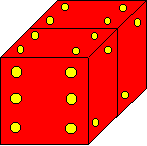
To create a block to use in these mazes, take two dice and stick them together. One easy way to do this is to wrap the dice in Scotch tape. Have the 6 face of one die showing at one end of the block and the 1 face of the other die showing at the other end. The numbers on the dice have no meaning in the first three of these mazes, but the “Other-End-Up Maze” needs a block with one end distinguished from the other. The clearest way to distinguish the ends is with the 6 and 1 faces.
Your block should look something like the picture at the left. Well, it won’t really look that bad. That’s just the best picture I can draw using MS Publisher. In that diagram, each of the long sides has the same two numbers. That isn’t really necessary, but you might follow that example just in case someone comes up with a new maze that makes use of the numbers.

Richard Tucker’s Original Rolling-Block Maze

Besides creating the block for this maze, you also have to print out a full-size diagram of the maze. You can click here to go to that diagram and then print it.

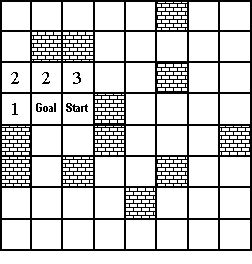Small Version of Maze At the left is a small illustration of the maze. The numbers in the illustration are only for the example given below. Those numbers don’t appear in the full-size diagram of the maze.
To begin the maze, stand the block vertically on the square marked Start. You then must roll the block around the maze until it is standing vertically on the square marked Goal. At no time can any part of the block land on any of the squares with the brick wall pattern.
Here is an example: From Start there is only one possible move, to tip the block west. It now lies horizontal and covers the square labeled Goal and the square numbered 1. The second move can only be to roll the block north, so it lies across the two squares numbered 2. On the third move you must roll the block to the east. It is now standing vertically on the square numbered 3. For the fourth move you have a choice, to tip the block to the east or to the south. And so on. Click here for the solution.

I wrote about this maze in a column in the December 1998 issue of Mensa Bulletin. Tucker’s maze was also a Puzzle-of-the-Week on Ed Pegg’s site, www.mathpuzzle.com. Ed received a great deal of response about the maze. A correspondent in Finland even created a new rolling-block maze (which subsequently appeared as another Puzzle-of-the-Week). Clearly, this concept of a rolling block had started something. So—next we have . . .

Robert Abbott’s Rolling-Block Maze

I thought Tucker’s maze was such a great idea that I created my own rolling-block maze. You can click here for a diagram of the maze, then print it. The rules are the same as those in Tucker’s maze. And you can click here for the solution.

My rolling-block maze has extensive false paths and loops—something I try to have in all my mazes. Richard Tucker immediately picked up on the importance of these diversions from the true path. So—now we have . . .

Richard Tucker’s Hayling Island Maze

This rolling-block maze has the name “Hayling Island” because that’s where Tucker created it.

This is, so far, the hardest of these rolling-block mazes. After you’ve gone a short distance from Start, you’ll find yourself entangled in a thicket of interlocking loops. Even if you find your way through that thicket, more confusion lies ahead.

Click here for a diagram of the maze, then print it. The rules are the same as those in the original rolling-block maze. And you can click here for the solution.

Robert Abbott’s Other-End-Up Maze

This maze introduces a change in the rules for rolling-block mazes. Then the “Rolling-Slab” and the other mazes that follow introduce changes in the shape of the thing that rolls plus additional changes in rules.

In the Other-End-Up maze you use the normal rolling block, but you must be able to distinguish one end of the block from the other. I’ll assume you have a block like the one in the diagram shown above. That block has a 6 face on one end and a 1 face on the other.

Click here for a diagram of the maze then print it. Place the block upright on the square marked Start/Goal. The face with 1 should be on top. Roll the block around the board, avoiding the squares with the brick pattern. The object is to get the block to an upright position back on the Start/Goal square, but this time with the 6 face on top.

Here’s an example: from Start/Goal roll south, then east, north, east, east, east, east, south, west, north, west, west, west, west. You’re now back on Start/Goal and the block is standing upright, but the 1 is still on top. So—that path doesn’t solve the maze.

This maze appeared as a Puzzle-of-the-Week on mathpuzzle.com, and only three people solved it! Just to drive everyone else crazy, I won’t provide a solution here. But I will mention that the shortest solution takes 49 moves. I also won’t give solutions for any of the following mazes.

Two Rolling-Slab Mazes

Ed Pegg has consistently nurtured the creation of these rolling-block mazes. Every maze in this section, plus others that I didn’t use, has appeared as a Puzzle-of-the-Week on his site. (That’s the site’s nifty new logo on the right.)

One week Ed received two Rolling-Slab mazes from two different people. Each used a shape made of four dice taped together to form a 2x2x1 slab. I think it’s pretty amazing for two people to come up with the same original idea at the same time. One maze was from maze designer Adrian Fisher and the other from Erich Friedman. Friedman is an Associate Professor of Mathematics at Stetson University, in DeLand, Florida. You might check out his puzzle page, especially the Mirror Puzzles, which have the appearance of mirror mazes.

After you’ve taped together four dice to form the slab, click here to get to Adrian Fisher’s maze, then print it. Place one of the narrow sides of the slab on the two squares marked Start. Then roll the slab around the board until you can get a narrow side onto the two squares marked Goal. The shortest solution takes 28 moves.

Click here to get to Erich Friedman’s maze and print it, then follow the same rules. The solution to this maze takes 54 moves.

Adrian Fisher’s Chasm Maze

This is a really great idea by Adrian Fisher.

Tape together three dice to form a 3x1x1 block. Click here to get to the maze and then print it. Place the long block upright on the square marked Start and roll it around until you get it upright on the square marked Goal.

There is an interesting change of rules in this maze. The shaded squares don’t act as barriers the same way as the squares with brick patterns do in the other mazes. Here, you may not have the block upright on one of the shaded squares. You also may not have the block lying down if a die at either end is over a shaded area. However, the block can span one of the shaded squares. That is, if the die at one end is on a white square, and the die at the other end is on a white square, then it’s alright for the die in the middle to be over a shaded square.

The shortest solution takes 20 moves.

Richard Tucker’s Minimal Maze

This is a creation in something of a “minimalist” tradition. Richard Tucker designed a diagram of only 8x8 squares that is almost bare. There are only three barriers on the diagram. But this is the most complex of all these rolling-block mazes.

This maze uses a block of six dice taped together to form a 3x2x1 block. Click here to get to the maze and then print it. Place the block so it is standing on one of its long edges, and it lies across the three squares marked Start. The object is to roll the block until it stands on a long edge and lies across the three squares marked Goal. No part of the block can land on any of the squares with the brick pattern.

Solving this maze is an interesting experience. After you leave Start you travel for a long distance without having to do much thinking. The only false paths you encounter are very short. Then, after the 18th move, the maze suddenly opens up and you’re overwhelmed with false paths and loops. Something similar happens if you solve the maze backwards from Goal. Here you go for 20 moves before you encounter any complexity.

Richard Tucker tells me that the shortest solution is 59 moves. But you should be happy if you can find any solution. So far, the shortest solution I’ve found is 67 moves.

Back to the home page.